How does Facebook suggest new long lost friends? And, how does Google get your searches right so often. The answer is Graph Theory, an area of mathematics being investigated by Prof. Josef Lauri. Dr Claude Bajada finds out more.
A mathematician sits alone at his desk. Hunched over a stack of papers he plays with numbers as a child would work at a jigsaw puzzle. The scene dematerialises in front of your eyes. A new reality builds up. People are connected to one another by virtual links. They have access to every convenience at the click of a button. Computers know their likes and dislikes. Algorithms find cures for diseases. Security agencies know your every step. The world is safe. The world is good. There is nowhere to hide.
As I interview mathematician Prof. Josef Lauri (University of Malta), these thoughts race through my mind. Lauri works on Graph Theory, which involves solving complex puzzles. He starts the interview by drawing an odd shape on a blank piece of paper; dots with lines connecting them. While drawing and explaining a particularly difficult problem he is tackling, Lauri tells me that his fondness for Graph Theory is akin to his son’s passion for the football players Lionel Messi and Cristiano Ronaldo. ‘Neither of them have solved any medical problem, but they have made a lot of people happy.’ Abstract mathematical problems make pure mathematicians like Lauri happy. But the difference between a goal by Messi and a puzzle of the pure mathematician is that the joys of the mathematician can change the world.
Leonhard Euler established Graph Theory in 1737. Like Lauri, Euler set out to solve a puzzle. Königsberg (now Kaliningrad, part of Russia) was a city with two islands and seven bridges. Was it possible to walk through the city using each bridge only once? Euler created a mathematical description of the way objects (land) related to one another (bridges). We use the term ‘node’ to describe the land areas in Königsberg and the term ‘edge’ to describe the bridges. By abstracting the problem into a mathematical framework, Euler was able to prove that there was no way of taking the suggested path. More importantly, this solution allowed other problems to be solved.
Computers revolutionised Graph Theory. Until then, it was ‘a specialised subject with no applications. The applications of mathematics were oriented towards the physical sciences,’ says Lauri. But in 1996 a paradigm shift occurred. Larry Page and Sergey Brin used Graph Theory to organise the world wide web. They developed PageRank and Google was born. In the old days, search engines ranked pages by the amount of keywords present on that page. If someone looked up the phrase ‘Think magazine’ on the Internet, search engines would crawl the web looking for websites that contained those keyword. The search engine assumed that the page that used that phrase the most was the most important result. A problem with this method was that a site that contains a keyword many times was not necessarily the most important site. Spammers could pad their site with keywords of their choice and appear high on the ranking. Brin and Page’s new algorithm ranked websites (the nodes of their graph) according to the number of other sites that linked to them (the edges). Lauri tells me that to understand the way this is done one needs to learn about fancy things like eigenvectors, but PageRank, like much in Graph Theory, is simple to understand: a page is important if other important pages link to it.
Like Google, other Internet companies have seen value in using Graph Theory. Facebook and LinkedIn create social networks, in other words, social graphs. Each person is a node and a ‘friendship’ is an edge. Many people have experienced looking up an old school friend on Facebook. The site then starts recommending other people from your class. An algorithm tailors its suggestions to your specific situation by using your social graph. ‘It looks simplistic but it is amazing how well it works, you can see it yourself!’ exclaims Lauri. In this way advertising is becoming personalised. Digital assistants such as Siri, Cortana, and Google Now suggest new movies for you to watch using the same principles that underlie Lauri’s puzzles. Sociologists caught the bug before the modern day Internet giants. They have been analysing sociograms since the 1930s. They analyse social problems by looking for abnormal network structure. The reach of Graph Theory has been immense, scientists now use Graph Theory to analyse medical data and find new ways of curing diseases.
Governments have jumped on the bandwagon. They use Graph Theory for public security. In 2001, the National Security Agency (NSA) started collecting metadata from US telephone calls. This allowed them to build a communications network that is like a Facebook friendship network. Imagine having access to everyone’s Facebook network. NSA have access to this level of information. The NSA analyses this data using Graph Theory coupled with raw computing power. The agency can then root out suspected criminals and prevent terrorist activity. But, there is always collateral damage. Using the mathematics of Graph Theory, governments know a lot more about their citizens than ever before.
As the interview ends, the dystopic visions disassemble. Once again, I see the pure mathematician sitting in front of me. The interview has opened a door to perceive both the amazing and scary applications of Lauri’s work. When I leave the room I cannot help but think: all the giants of our modern world, Facebook, Google, and NSA, are standing high on the shoulders of the work of pure mathematicians.
What is Graph Theory?
Graph Theory is a branch of Mathematics that describes how networks work. Networks are basically the relationship of a group of separate objects to one another. For example, five objects labeled as 1, 2, 3, 4, 5 can interact as follows:
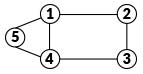
Each of the objects are called vertices or nodes. The lines that connect them are called edges or links. This graph can then be used to describe many different types of networks. For example, the nodes could represent people and the edges may be friendships. Alternatively they could be websites and weblinks. The way the graph is drawn does not matter as long as the connections are the same.
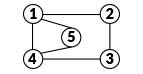
The graph can either be described as it is, or more often, it can be transformed into a matrix in order to do more complicated mathematics on it. This can identify which node is more important (a hub) or which group of nodes belong to the same group (or cluster). For example, in Think magazine’s facebook network. The University of Malta page is a hub in the same cluster as Think’s page.
Further reading
- Barabasi, A. (2015). Network Science. [online] Barabasi.com. Available here.
- Brin, S. and Page, L. (1998). The anatomy of a large-scale hypertextual Web search engine. Computer Networks and ISDN Systems, 30(1-7), pp.107-117.
- Seven Bridges of Königsberg – Woodside High School. (2013). Video available here.




Comments are closed for this article!